Rechenschaltungen
Halbaddierer (HA)
Symbol
Schalttabelle

Simulation mit Locad
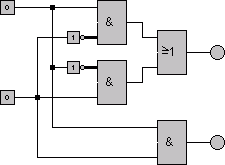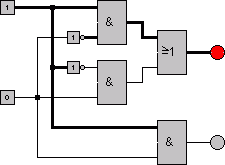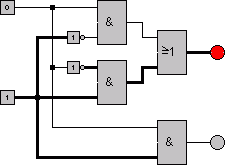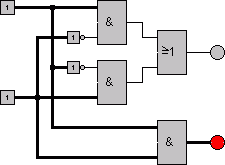
animiert
Aufbau mit Logitron-Bausteinen

animiert
Aufgabe:
- Welche Grundbausteine befinden sich in einem HA-Baustein?
- Nimm die ICs 7408 und 7486, zwei LEDs mit Vorwiderständen und einige Kabel und baue einen Halbaddierer.
- Der Halbaddierer kann auch mit einem XOR und einen UND-Baustein realisiert werden; denn es ist
s = a ⊕ b und ü = a ∧ b.
Zeichne den Schaltplan und baue die Schaltung auf. -
Entwirf einen Halbsubtrahierer:
0 - 0 = 0 mit Übertrag 0
0 - 1 = 0 mit Übertrag 1 Erklärung dazu siehe unten
1 - 0 = 0 mit Übertrag 0
1 - 1 = 0 mit Übertrag 0
Woran ist zu erkennen, dass das Ergebnis negativ ist?
1-Bit-Volladdierer (VA)
Die Addition zweier mehrstelliger Binärzahlen erfordert an jeder Stelle einen Addierer mit drei Eingängen (Volladdierer genannt), weil der Übertrag der vorangehenden Stelle addiert werden muss.
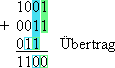
Symbol
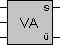
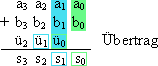
Schalttabelle

Simulation mit Digital Works 2.0
 animiert
animiert
Aus der Schalttabelle ergeben sich Terme für die Summe s und den Übertrag ü, die vereinfacht werden.
s =
c∧b∧a
∨ c∧b∧a
∨ c∧b∧a
∨ c∧b∧a
=
c∧((b∧a)∨(b∧a))
∨ c∧((b∧a)∨(b∧a))
=
c∧((a∧b)∨(b∧a))
∨ c∧((b∧a)∨(a∧b))
=
c∧(a⊕b) ∨ c∧(b⊕a)
wie unter Logik gezeigt
=
c⊕(b⊕a)
= (a⊕b)⊕c
c =
c∧b∧a
∨ c∧b∧a
∨ c∧b∧a
∨ c∧b∧a
=
(c∨c)∧(b∧a)
∨ c∧((b∧a)∨(b∧a))
=
(b∧a) ∨ c∧(a⊕b)
Aufgabe:
- Mache klar, dass die Schaltung aus zwei Halbaddierern HA und einem zusätzlichen ODER besteht.
- Zeichne den Schaltplan für einen Volladdierer.
- Simuliere den Volladdieren am Computer.
- Baue einen Vollassieren mit zwei XOR- und einem UND-Bausteien auf.
4-Bit-Volladierer (VA4)
Vier 1-Bit-Volladdierer werden in Reihe geschaltet, so dass zwei 4-Bit-Zahlen addiert werden können. Auch an der letzten Stelle (Bit 0) wird ein 1-Bit-Volladdierer verwendet; so können mehrere 4-Bit-Volladdierer in Reihe geschaltet werden, um 8-Bit-Zahlen oder mehrstellige zu addieren (Kaskade).
Kaskade

74283 als Volladdierer
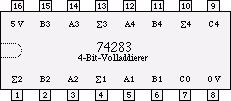
Locad-Modul (Simulation)

Beachte: Da sich nun an der letzten Stelle (Bit 0) statt eines Halbaddieres ein Volladdierer befindet, muss am Übertragseingang (Carry-Input C0) des rechten 4-Bit-Volladdieres manuell eine "0" angelegt werden.
Zahlen
Nach der Regel a - b = a + (-b) wird die Subtraktion auf die Addition einer negativen Zahl zurückgeführt. Aber wie sieht eine negative Zahl aus?
Weil 1111+0001 beim Addieren 0000 ergibt, was bei unseren "normalen" Zahlen -1 + 1 = 0 enspricht, soll 1111 die Zahl vor 0000 sein, also der dezimalen -1 entsprechen.
Bezogen auf eine 4-Bit-Zahl wird man die 16 Kombinationen (möglichst fair) aufteilen in positive Zahlen, negative Zahlen und Null.
0000 bleibt Null, 0001 bleibt 1 usw.
Die Zahlen, die mit einer "1" beginnen, das ist die Hälfte aller 4-Bit-Zahlen, betrachten wir als negativ. Die anderen als positiv bzw. 0000 speziell als Null.
Es gibt also 8 negative Zahlen und 7 positive und Null. Das ist wenig! Um einige größere Anzahl zu bekommen, um sinnvoll rechnen zu können, müssen mehr als 4 Bits benutzt werden.
| Anzahl Bits | Anzahl Zahlen | größte positive Zahl |
|---|---|---|
| 4 | 24 = 16 | 7 |
| 8 | 28 = 256 | 127 |
| 16 | 216 = 65536 | 65536 |
| 32 | 232 = 4294967296 | 2147483647 |
| 64 | 264 = 18446744073709551616 | 9223372036854775807 |
Immer besteht aber das Problem, dass beim Rechnen das Ergebnis so groß wird, dass die größte darstellbare Zahl überschritten wird. Dann liegt ein Überlauf vor, den der Programmierer erkennen muss.
Um sehr große Zahlen und sehr kleine (also Bruchteile) zu beschreiben, benutzt man Festkommazahlen mit Exponentialschreibweise wie 3.1862792*10-4 eingeführt. Die Anzahl der dabei verwendeten Ziffern bestimmt die mögliche Genauigkeit.
Negative Zahlen
Wenn zu einer positiven Zahl die zugehörige negative Zahl (Gegenzahl) gefunden werde soll, ist das Zehnersystem einfach: -37 ist das Negative von 37, denn -37 + 37 = 0.
Und wie ist das bei Binärzahlen?. Es ist leicht, zu einer Zahl eine andere zu finden, deren Summe 1111 ergibt. Dazu müssen nur alle Ziffern "umgedreht" werden:
0000 0001 0010 0011 0100 0101 0110 0111 +1111 +1110 +1101 +1100 +1011 +1010 +1001 +1000 ----- ----- ----- ----- ----- ----- ----- ----- 1111 1111 1111 1111 1111 1111 1111 1111Es muss nur zusätzlich die Zahl 0001 addiert werden, dann ergibt sich 0000.
0000 0001 0010 0011 0100 0101 0110 0111
+1111 +1110 +1101 +1100 +1011 +1010 +1001 +1000
+0001 +0001 +0001 +0001 +0001 +0001 +0001 +0001
----- ----- ----- ----- ----- ----- ----- -----
0000 0000 0000 0000 0000 0000 0000 0000
Die "umgedrehte Zahl" (Zweierkomplement genannt) plus 0001 ist die Gegenzahl:-0110 = 1001+0001 = 1011; allgemein - d c b a = d c b a + 0 0 0 1.
Aufgabe:
- Bestimme den Grundbaustein der das Komplement (0 wird 1, 1 wird 0) bildet?
- Zeichne den Schaltplan für das Zweierkomplement einer 4-Bit-Zahl.
- Simuliere den Aufbau des Zweierkomplement einer 4-Bit-Zahl am Computer.
Aufgabe: Erläutere:
-
Welche Rechenaufgabe wird im folgenden Locad-Schaltbild bearbeitet?
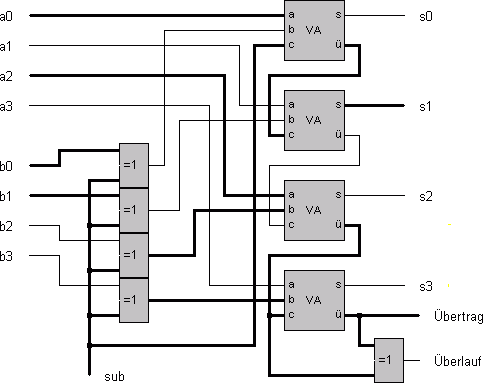
- Warum werden XOR-Bausteine verwendet?
- Was ergibt sich für sub=0 bzw. sub=1?
- Welche Bedeutung das Signal "Überlauf"?
- Wann geht es auf "1"?