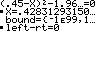Schätzen

Schätzen: Vertrauensintervall für den Stichprobenumfang bei einer Summe (Summenbildung)
[Klett LS Stochastik S.143, Bsp.2b]
Y = x1 + ... + xn
µx = 0,4 ist bekannt
σx = 0,08 ist bekannt
α = 0,05
Die Summenwerte Y sind normalverteilt mit
μy = 0,4·n
σy = 0,08·n

220 soll im Vertrauensintervall
[μy-2·σy; μy+2·σy] = [0,4·n−2·0,08·n; 0,4·n+2·0,08·n] liegen.
Für das größtmögliche n gilt
220 = 0,4·n+2·0,08·n
MATH 0:Solver...

.4*X-2*.08*√(X)-220
ENTER
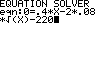
Startwert
800 SOLVE
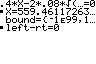
Für das kleinstmögliche n gilt
220 = 0,4·n+2·0,08·n

... Rechenzeichen ändern
+ ENTER
ALPHA SOLVE
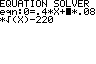
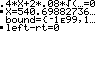
Schätzen: Vertrauensintervall für Erwartungswert bei bekannter Standardabweichung und bekanntem Mittelwert
[Klett LS Stochastik S.143, Bsp.1b]
σx = 9 ist bekannt
α = 0,05
x = 143,2 wird in einer Stichprobe mit Umfang n = 26 ermittelt
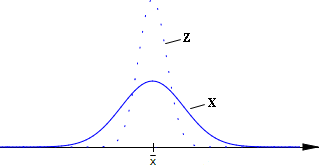
Die Mittelwerte Z = x1 +...+ xn n sind normalverteilt mit μz = μx = 143,2 und σz = σx n ≈ 1,77.

Das Vertrauensintervall für den Erwartungswert ist [μz-2·σz; μz+2·σz] ≈ [139,7; 146,7].
Schätzen: Vertrauensintervall für Wahrscheinlichkeit bei bekannter relativer Häufigkeit
Stichprobenumfang n = 2000
Vorinformation h = 0,45 = 45%
Signifikanznineau α = 0,05 und Vertrauenszahl γ = 1–α = 0,95
Also c = Φ-1( 1- α2 ) = Φ-1( 1+γ2 ) = 1,96
Grenzen des Vertrauensintervalls p1 und p2 sind die Lösungen der Gleichung
(h – p)² = c² · p·(1-p) n .
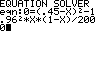
Startwert kann zum Beispiel h = 0,45 sein.
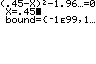
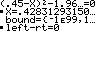
Die zweite Lösung wird nun rechts von h vermutet.

p liegt zu 95% im Vertrauensintervall [0,428; 0,472].
Schätzen: Mindeststichprobenumfang bei vorgegebener maximaler Abweichung
Intervalllänge d = 0,05
Signifikanzniveau α = 0,05 (γ = 1–α = 0,95), also c = 1,96 (wie oben)
n ≥ 1,96²d² = 1536,64 ≥ 1536
Der Umfang der Stichprobe muss mindestens 1536 sein.
1.96 x2 / .05 x2