Waagerechter Wurf
Eine Kugel rollt mit der Geschwindigkeit v0 über eine Tischkante.
1. Wo befindet sie sich nach der Zeit t?
2. In welche Richtung bewegt sie sich zur Zeit t?
3. Welche Geschwindigkeit besitzt sie zur Zeit t?
Gegeben sind v0 = 10 m/s und g = 10 m/s2.
Wir wollen das Geschehen in den ersten 5 s (sekundenweise) beobachten.
v0 := 10: g := 10: tmax := 5:
Anders als Donald Duck bei der Eichhörnchenjagd bewegt sich die Kugel zugleich nach rechts (mit der konstanten Geschwindigkeit) und nach unten (im freien Fall).
Wir legen die Tischkante in den Koordinatenursprung und können die x- und die y-Koordinaten des Kugelmittelpunktes zur Zeit t dann nach den Formeln
x = v0t
berechnen. Wir erhalten eine Liste von Punkten.
p := [v0*t, -1/2*g*t^2] $t=0..tmax;
![]()
Für die grafische Darstellung werden Punkt-Objekte erzeugt.
punkt := proc() begin plot::Point2d([v0*args(1), -1/2*g*args(1)^2],args(2..args(0))); end:
punkt(t) $t=0..tmax;
![]()
Diese Punkte werden in einem Diagramm dargestellt. (Lösung zu Frage 1)
plot(punkt(t) $t=0..tmax)
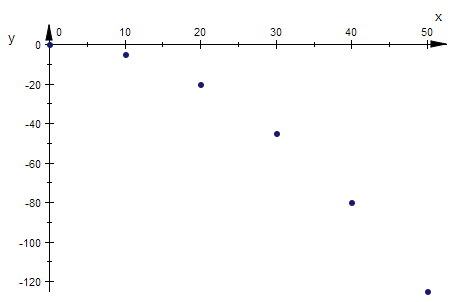
Zur Veranschaulichungen werden wir die Kugel - wie Donald - waagerecht weiter schweben lassen.
Aber das ist ja - wie Herr Duck schließlich auch bemerkt - nur die halbe Wahrheit: Jenseits der Tischkante fällt die Kugel "frei" senkrecht nach unten.
punktHor := proc(t) begin plot::Point2d([v0*t,0 ],args(2..args(0))); end:
punktVer := proc(t) begin plot::Point2d([0 ,-1/2*g*t^2],args(2..args(0))); end:
plot(
punkt (t ) $t=0..tmax,
punktHor(t,Color=RGB::Red ) $t=0..tmax,
punktVer(t,Color=RGB::Blue) $t=0..tmax
)

Das müssen wir "live" sehen.
plot(
punkt (t, t=0..nops(p) ),
punktHor(t, t=0..nops(p), Color=RGB::Red ),
punktVer(t, t=0..nops(p), Color=RGB::Blue)
)
Was wissen wir über x, was wissen wir über y?
Beide hängen von t ab und hängen folglich "zusammen".
gleichungen := {x = v0*t, y = -1/2*g*t^2};
![]()
Nach t aufgelöst und eingesetzt ergibt sich:
loesung := solve(gleichungen,{t,y});
kurve := x --> y | loesung;
plot(plot::Function2d(kurve,x=0..60)):
![]()
![]()
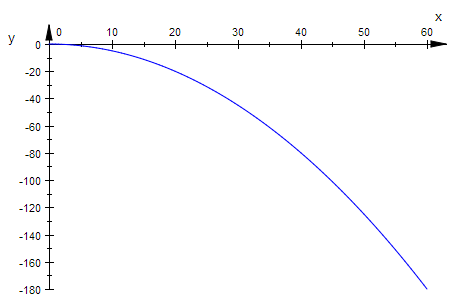
Die Kugel bewegt sich nach rechts mit der konstanten Geschwindigkeit v0 und nach unten im freien Fall mit der immer größer werden Geschwindigkeit -gt.
Die wirkliche Bewegungsrichtungsrichtung liegt dazwischen und ergibt sich durch Addition der horizontalen
und der vertikalen Geschwindigkeitsvektoren. (Lösung zur Frage 2)
v := [v0,-g*t] $t=0..tmax
![]()
Im Schaubild soll die Geschwindigkeit durch einen Pfeil dargestellt werden, der an der Kugel angetragen wird.
pfeil := proc(t)
local pos;
begin
pos := [v0*t, -1/2*g*t^2];
plot::Arrow2d(
pos, // Anfangspunkt
zip(pos,[v0,-g*t],_plus), // Endpunkt
args(2..args(0)) // Optionen
);
end:
Schauen wir mal.
plot(
punkt(t ) $t=0..tmax,
pfeil(t,Color=RGB::Blue) $t=0..tmax
)
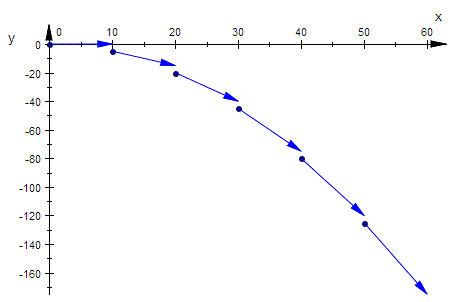
plot(
pfeil(t, t=0..tmax, Frames=100, Color=RGB::Red),
punkt(t, t=0..tmax, Frames=100)
)
Und jetzt alles zusammen - zusätzlich mit den Geschwindigkeitsvektoren einer frei fallenden und einer dahin schwebenden
Kugel. Zunächst eine verallgemeinerte Version des pfeil-Programms:
pfeil := proc(tparam,vx,vy)
local pos;
begin
pos := ([v0*t,-1/2*g*t^2]) | t=tparam;
return;
plot::Arrow2d(
pos, // Anfangspunkt
zip(pos,([vx,vy]) | t=tparam,_plus), // Endpunkt
args(4..args(0)) // Optionen
);
end:
Und dann die Grafik.
frames := 100:
plot(
Kurve,
pfeil(t, v0, -g*t, t=0..tmax, Frames=frames, Color=RGB::Red),
pfeil(t, v0, 0, t=0..tmax, Frames=frames, Color=RGB::Green),
pfeil(t, 0, -g*t, t=0..tmax, Frames=frames, Color=RGB::Green),
punkt(t, t=0..tmax, Frames=frames)
)
Der Betrag der Geschwindigkeit ergibt sich aus der Länge des Geschwindigkeitsvektors, und die ist nach dem Satz des Pythagoras .
Wir lassen die Geschwindigkeit für die ersten Sekunden (0 bis tmax) berechnen.
vbetrag := [t, sqrt(v0^2 + (g*t)^2)] $t=0..tmax
![]()
plot(plot::Point2d(vbetrag[t],PointSize=2) $t=1..tmax+1)

Der Betrag der Geschwindigkeit ergibt sich aus der Länge des Geschwindigkeitsvektors, und die ist nach dem Satz des Pythagoras .
Wir zeichnen also den Graphen der Funktion x ↦ über der Definitionsmenge ℝ+.
Und zum Vergleich die Geschwindigkeitsfunktion x ↦ einer frei (über die Kante) fallenden Kugel (in rot).
Wenn die Kugel die Tischkante verläßt, beträgt die Geschwindigkeit 10 m/s. Das ist ihre horizontale Geschwindigkeit. Dann fällt sie und wird immer schneller. Sie wird so schnell, dass die Anfangsgeschwindigkeit schließlich kaum noch eine Rolle spielt.
plotfunc2d(sqrt(v0^2 + (-g*t)^2),
g*t,
t=0..5)
