Waagerechter Wurf und Schiefer Wurf
Ein Ball rollt.
v := 3;
s := t -> v*t;
P := plot::Point2d(s(t),0,PointSize=3,Color=RGB::Red, t=-0..10):
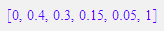
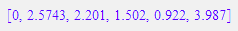
Animation. (Das Schaubild Doppelklicken und die Animation starten.)
plot(P):
Ein Ball fällt.
g := 10:
s2 := t -> -g/2*t^2;
Q := plot::Point2d(0,s2(t),PointSize=3,Color=RGB::Green, t=-0..10):

plot(Q)
Ein Ball rollt und ein Ball fällt.
plot(P,Q)
Ein dritter macht beide Bewegungen zugleich.
R := plot::Point2d(s(t),s2(t),PointSize=3,Color=RGB::Blue, t=0..10):
plot(P,Q,R)
Was wissen wir über x, was wissen wir über y?
Beide hängen von t ab und hangen folglich "zusammen".
x = s(t), y =s2(t)
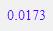
Nach t aufgelöst und eingesetzt ergibt sich:
temp := solve({x = s(t), y=s2(t)},{t,y});
f := x --> y | temp;
F := plot::Function2d(f,x=0..30):

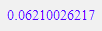
plot(P,Q,R,F)
Wir verändern die Ausgangsituation.
Jetzt ist der rollende Ball zu spät dran. Er ist zur Zeit t nicht an der Stelle s(t), sondern erst bei s(t-4).
Auch der fallende Ball ist zu spät. Er ist zur Zeit t bei s2(t-4) - und noch dabei, auf seine größte Höhe zu steigen.
Der dritte Ball macht es beiden nach.
dt := 4:
P := plot::Point2d(s(t-dt),0 ,PointSize=3,Color=RGB::Red, t=-0..10):
Q := plot::Point2d(0 ,s2(t-dt),PointSize=3,Color=RGB::Green, t=-0..10):
R := plot::Point2d(s(t-dt),s2(t-dt),PointSize=3,Color=RGB::Blue, t=0..10):
plot(P,Q,R)
Jetzt verlegen wir den Startpunkt des dritten, blauen Ball in den Ursprung, indem wir alle x-Koordinaten um 12 und alle y-Koordinaten um 80 erhöhen.
Wieso ist eigentlich dx=12 und dy=80, wenn dt=4 ist?
dt := 4:
dx := 12: // allg s(dt)
dy := 80: // allg s2(dt)
P := plot::Point2d(s(t-dt)+dx,0 +dy,PointSize=3,Color=RGB::Red, t=-0..10):
Q := plot::Point2d(0 +dx,s2(t-dt)+dy,PointSize=3,Color=RGB::Green, t=-0..10):
R := plot::Point2d(s(t-dt)+dx,s2(t-dt)+dy,PointSize=3,Color=RGB::Blue, t=0..10):
plot(P,Q,R)
Was wissen wir jetzt über x, was wissen wir über y?
Beide hängen von t ab und hangen folglich "zusammen".
x=s(t-dt)+dx, y=s2(t-dt)+dy

Nach t aufgelöst und eingesetzt ergibt sich:
temp := solve({x=s(t-dt)+dx, y=s2(t-dt)+dy},{t,y});
f := x --> y | temp;
F := plot::Function2d(f,x=0..30):
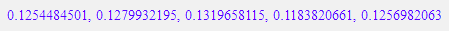
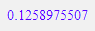
plot(P,Q,R,F)