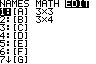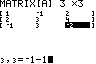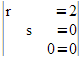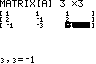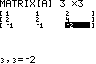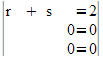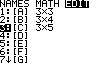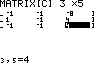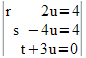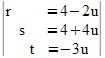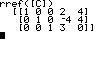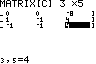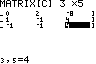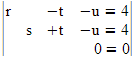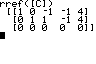Lineare Gleichungssysteme
Das lineare Gleichungssystem hat genau eine Lösung
|
Die Geraden und h schneiden sich in einem Punkt:
|
MATRX EDIT 1:[A]
|
|
|
|
3x3 Eingabe spaltenweise |
|
|
(genau eine Lösung) |
QUIT MATRX MATH B:rref( MATRX NAMES 1:[A] ENTER |
|
Das lineare Gleichungssystem hat keine Lösung
|
Die Geraden und h schneiden sich nicht:
|
MATRX EDIT 1:[A]
|
|
|
|
3x3 Eingabe spaltenweise |
|
|
|
QUIT MATRX MATH B:rref( MATRX NAMES 1:[A] ENTER |
|
Das lineare Gleichungssystem hat unendlich viele Lösungen
|
Die Geraden und h sind identisch:
|
MATRX EDIT 1:[A]
|
|
|
|
3x3 Eingabe spaltenweise |
|
|
(unendlich viele Lösungen) |
QUIT MATRX MATH B:rref( MATRX NAMES 1:[A] ENTER |
|
Weitere Beispiele
|
Die Ebenen E und F schneiden sich:
|
MATRX EDIT 1:[C]
|
|
|
|
3x5 Eingabe spaltenweise |
|
|
u beliebig (unendlich viele Lösungen) |
QUIT MATRX MATH B:rref( MATRX NAMES 1:[C] ENTER |
|
|
Die Ebenen E und F sind parallel:
|
|
|
|
|
|
|
|
Die Ebenen E und F sind identisch:
|
|
|
|
(unendlich viele Lösungen) |
|
|