Normalisierung
Man kann sich eine Datenbank als eine Tabelle vorstellen, in der alle Daten in Zeilen und Spalten angeordnet sind.
Wir betrachten als Beispiel den naturwissenschaftlichen Unterricht der Gymnasien einer Stadt.
LEHRER (KUERZ, NAME, TITEL, ANREDE, SCHULE, SCHULNAME, FACH, KLASSE)
| KUERZ | ANREDE | ANREDE | NAME | SCHULE | SCHULNAMME | FACH | KLASSE |
| FI | Herr | StR | Fisch | OHG | Otto-Hahn-Gymnasium | CH PH |
9a |
| KA | Herr | StD | Kater | FKG | Felix-Klein-Gymnasium | CH PH |
8c | CH PH |
9a |
| KA | Frau | OStR' | Katze | OHG | Otto-Hahn-Gymnasium | BI MA |
8b |
Eine solche Tabelle wird in den meisten Fällen groß ausfallen und unübersichtlich sein. Dadurch besteht dann die Gefahr von Fehlern bei der Datenpflege.
Es ist sinnvoll, die Tabelle in mehrere kleinere Tabellen aufzuteilen. Dadurch können auch Zugriffsrechte einfacher definiert werden.
Das Aufteilen der Daten in getrennte Relationen soll so erfolgen, dass
- bei den üblichen Datenoperationen (DELETE, UPDATE, INSERT) keine fehlerhaften Ergebnisse entstehen
- bei Einführung neuer Daten (Attribute, Entities, Beziehungen) keine völlige Umstrukturierung erforderlich wird
- Redundanzen (doppelte Einträge) beseitigt werden
- ein verständliches Datenmodell für Benutzer und Programmierer entsteht.
Wir bringen die Tabelle mit Blick auf die Punkte 1 und 2 zunächst in die 1. Normalform.
Eine Relation ist in der 1. Normalform (1NF), wenn alle Attribute nur atomare Werte (und keine Nullwerte) beinhalten.
Als Primärschlüssel führen wir die Attributkombination KUERZ, SCHULE, FACH, KLASSE ein.
LEHRER_1NF (KUERZ, SCHULE, FACH, KLASSE, NAME, TITEL, ANREDE, SCHULNAME)
| KUERZ | SCHULE | FACH | KLASSE | ANREDE | TITEL | NAME | SCHULNAMME |
| FI | OHG | CH | 9a | Herr | StR | Fisch | Otto-Hahn-Gymnasium |
| FI | OHG | PH | 9a | Herr | StR | Fisch | Otto-Hahn-Gymnasium |
| KA | FKG | CH | 8c | Herr | StD | Kater | Felix-Klein-Gymnasium |
| KA | FKG | PH | 8c | Herr | StD | Kater | Felix-Klein-Gymnasium |
| KA | FKG | CH | 9a | Herr | StD | Kater | Felix-Klein-Gymnasium |
| KA | FKG | PH | 9a | Herr | StD | Kater | Felix-Klein-Gymnasium |
| KA | OHG | BI | 8b | Frau | OStR' | Katze | Otto-Hahn-Gymnasium |
| KA | OHG | MA | 8b | Frau | OStR' | Katze | Otto-Hahn-Gymnasium |
Die Tabelle enthält nun unnötig viele Wiederholungen. Zum Beispiel ist durch das Schulkürzel der Schulname eindeutig festgelegt, so dass er nicht immer wieder aufgeschrieben werden muss.

Wir erkennen weitere Abhängigkeiten und führen zusätzliche Tabellen ein.
Eine Relation ist in der 2. Normalform (2NF), wenn sie sich in der 1. Normalform befindet und jedes Nicht-Schlüssel-Attribut funktional abhängig ist vom Gesamtschlüssel, nicht aber von einzelnen Schlüsselteilen.
Die zweite Normalform kann also nur verletzt werden, wenn der Primärschlüssel aus mehr als einem Attribut zusammengesetzt ist.
In einer Relation heißt das Attribut B vom Attribut A funktional abhängig, falls zu jedem Wert des Attributs A genau ein Wert des Attributs B gehört (falls also die Abbildung f: A → B eindeutig ist).
Das Attribut B heißt voll funktional abhängig vom Gesamtschlüssel, wenn B von den zusammengesetzten Schlüsselattributen funktional abhängig ist, aber nicht von einem einzelnen Schlüsselteil.
In unserem Beispiel sind ANREDE, TITEL, NAME, SCHULNAME von einzelnen Schlüsselteilen abhängig. Wir entfernen diese Attribute aus der Tabelle und notieren den Zusammenhang in zusätzlichen Tabellen.
UNTERRICHT_2NF (KUERZ, SCHULE, FACH, KLASSE)
| KUERZ | SCHULE | FACH | KLASSE |
| FI | OHG | CH | 9a |
| FI | OHG | PH | 9a |
| KA | FKG | CH | 8c |
| KA | FKG | PH | 8c |
| KA | FKG | CH | 9a |
| KA | FKG | PH | 9a |
| KA | OHG | BI | 8b |
| KA | OHG | MA | 8b |
LEHRER_2NF (KUERZ, SCHULE, ANREDE, TITEL, NAME)
| KUERZ | SCHULE | ANREDE | TITEL | NAME |
| FI | OHG | Herr | StR | Fisch |
| KA | FKG | Herr | StD | Kater |
| KA | OHG | Frau | OStR' | Katze |
SCHULE_2NF (SKUERZ, SNAME)
| KUERZ | NAME |
| FKG | Felix-Klein-Gymnasium |
| OHG | Otto-Hahn-Gymnasium |
Auch in 2. Normalform enthält LEHRER noch Redundanzen. Durch Angabe des Titels ist auch die Anrede festgelegt, so dass sie nicht immer wieder aufgeschrieben werden muss.
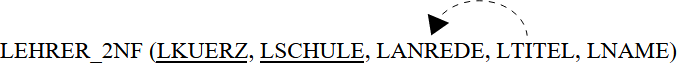
Eine Relation ist in der 3. Normalform, wenn sie sich in der 2. Normalform befindet und keine funktionale Abhängigkeit zwischen Attributen besteht, die nicht als Schlüssel definiert sind.
Nicht-Schlüssel-Attribute müssen also immer vom vollständigen Schlüssel funktional abhängig sein und nur von diesem.
Das erste Diagramm legt unmittelbar eine kurze (sogar etwas schärfere) Forderung nahe. In unserem Beispiel ist ANREDE nämlich transitiv abhängig vom Gesamtschlüssel.

Eine Relation ist in Boyce-Codd-Normalform (BCNF), wenn sie in der ersten Normalform ist und kein Attribut vom Schlüssel transitiv abhängt.
Ein Attribut B heißt transitiv abhängig vom Schlüsselattribut S, wenn B von einem Attribut A funktional abhängig ist und A wiederum funktional abhängig von S, jedoch umgekehrt S nicht von A.
LEHRER_2NF (KUERZ, SCHULE, TITEL, NAME)
| KUERZ | SCHULE | ANREDE | NAME |
| FI | OHG | StR | Fisch |
| KA | FKG | StD | Kater |
| KA | OHG | OStR' | Katze |
ANREDE_2NF (TITEL, ANREDE)
| TITEL | ANREDE |
| StR | Herr |
| StD | Herr |
| OStR' | Frau |
In diesem konstruierten Beispiel unterrichten alle Lehrer in jeder ihrer Klassen ihre beiden Fächer. Das führt zu unnötigen Doppeleinträgen.
Eine Relation ist in der 4. Normalform, wenn sie in der 2. Normalform ist und sie keine paarweise auftretenden mehrwertigen Abhängigkeiten enthält.
Ein Attribut B heißt mehrwertig abhängig vom Attribut A, falls zu jedem Attributwert von A dieselbe Menge von B-Werten gehört, unabhängig von den Werten der restlichen Attribute.
In unserem Beispiel ist das Attribut FACH mehrwertig abhängig vom Attribut Klasse:
| KUERZ | SCHULE | FACH | KLASSE |
| FI | OHG | CH | 9a |
| FI | OHG | PH | 9a |
| KA | FKG | CH | 8c |
| KA | FKG | PH | 8c |
| KA | FKG | CH | 9a |
| KA | FKG | PH | 9a |
| KA | OHG | BI | 8b |
| KA | OHG | MA | 8b |
Wir teilen die Tabelle auf. Dann ist nur eine Tabellenzeile zu bearbeiten, wenn Lehrer FI nicht mehr Klassenlehrer der 9a ist.
LEHRERFACH_4NF (KUERZ, SCHULE, FACH)
KUERZ,SCHULE ist Fremdschlüssel aus LEHRER.
| KUERZ | SCHULE | FACH |
| FI | OHG | CH |
| FI | OHG | PH |
| KA | FKG | CH |
| KA | FKG | PH |
| KA | OHG | BI |
| KA | OHG | MA |
LEHRERKLASSE_4NF (KUERZ, SCHULE, KLASSE)
| KUERZ | SCHULE | KLASSE |
| FI | OHG | 9a |
| KA | FKG | 8c |
| KA | FKG | 9a |
| KA | OHG | 8b |